
Under det senaste året har jag arbetat med flera olika projekt som verkligen visar hur AI kan användas för att optimera vitt skilda utmaningar. Exempelvis de där små återkommande aktiviteterna som man drar sig för att ta tag i för att man vet att: det tar tid, det måste göras och det är svårt att få det riktigt bra. Ett perfekt exempel på det är schemaläggning av personal på en restaurang som måste göras regelbundet. När det sen äntligen är klart så ändras plötsligt förutsättningarna som exemplevis att personal vill eller måste vara lediga – och man måste planera om för att hantera detta.
Optimering handlar ofta om att hitta en “tillräckligt bra” lösning på ett problem, då den bästa lösningen är väldigt svår eller omöjlig att hitta, eller för att det skulle ta för lång tid att söka igenom hela tillståndsrymden.
I denna artikel kommer jag att beskriva några viktiga beståndsdelar för att kartlägga, representera och lösa ett optimeringsproblem samt några exempel från verkligheten.
Problemen
Genom denna artikel kommer jag att referera till några olika problem som jag därför börjar med att kort beskriva här.
Schemaläggning av personal
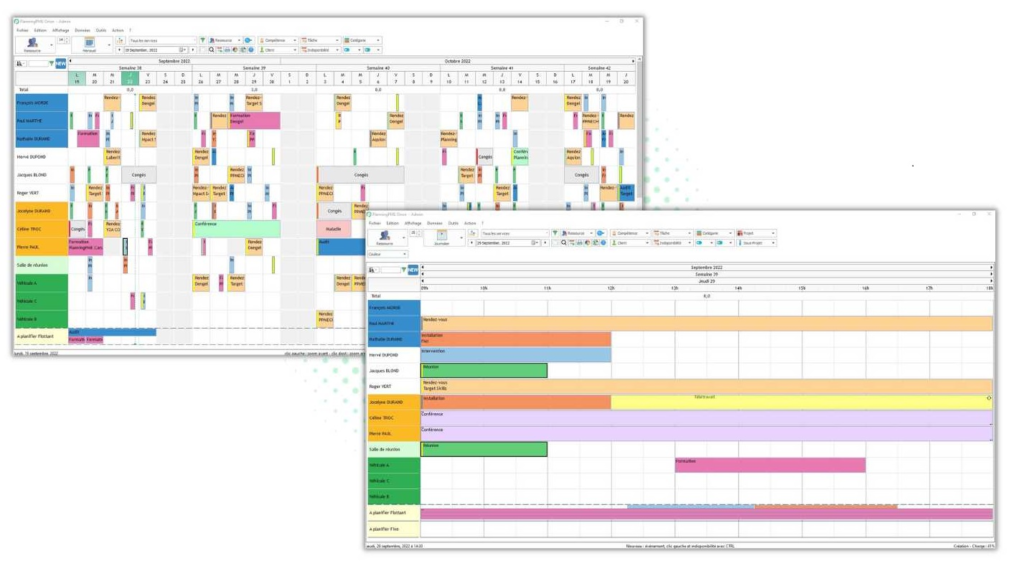
Nästan alla som har personal har behov av schemaläggning, dvs att planera vem som ska jobba och när de ska jobba. Utmaningarna är många, bland annat vilka tider det ska finnas personal i butiken eller restaurangen, hur många, vilka kan inte jobba på fredagar, vem jobbar bara 40%, vilka är juniora och måste alltid gå parallellt med någon mer erfaren person, ingen får jobba mer än 5 dagar i sträck, …
Det är dessutom ett problem som ökar exponentiellt i komplexitet med antalet personer som ska schemaläggas, antalet veckor schemat görs för, samt antal restauranger man hanterar.
Ruttoptimering
I sin enklaste form handlar detta om att hitta den “bästa” vägen från punkt A till punkt B. Men vad är det bästa vägen? Detta beror exempelvis på vilken tid jag vill resa från A, eller när jag senast vill vara framme vid B, vilka avgångar som finns från varje station, är det OK med byten under resan, ska resan bara göras med buss, hur mycket extratid måste det finnas vid byten, …
Det behövs inte särskilt många alternativa avgångar på varje station för att tillståndsrymden av möjliga lösningar ska bli väldigt stor.
Måltidsplanering

Vid träning och viktnedgång är måltiderna en viktig beståndsdel. Problemet här är att utifrån en databas med recept skapa en bra sammansatt måltidsdag bestående av upp till 6 måltider där man ska försöka pricka in en viss total dagsmängd energi med en specifik fördelning av fett, protein och kolhydrater.
Redan vid så få som 13 recept i databasen börjar man närma sig gränsen för vad en normal dator klarar av att söka igenom fullständigt för att hitta en lösning. Då behöver man vända sig till optimering.
Grunderna
Inom AI används optimeringstekniker för att hitta så bra lösningar som möjligt på olika problem genom att söka igenom ett mycket stort utrymme av möjliga lösningar, den så kallade “tillståndsrymden”. I praktiken handlar det om att sökalgoritmen försöker minimera eller maximera en viss målvariabel – som att minska kostnader, restid eller kalorier.
Antag att vi har grafen nedan. Den representerar en väldigt enkel tillståndsrymd som bara består av X. Beroende på vilket värde X har så räknar vi fram ett värde eller poäng, Y, som anger hur bra X är.
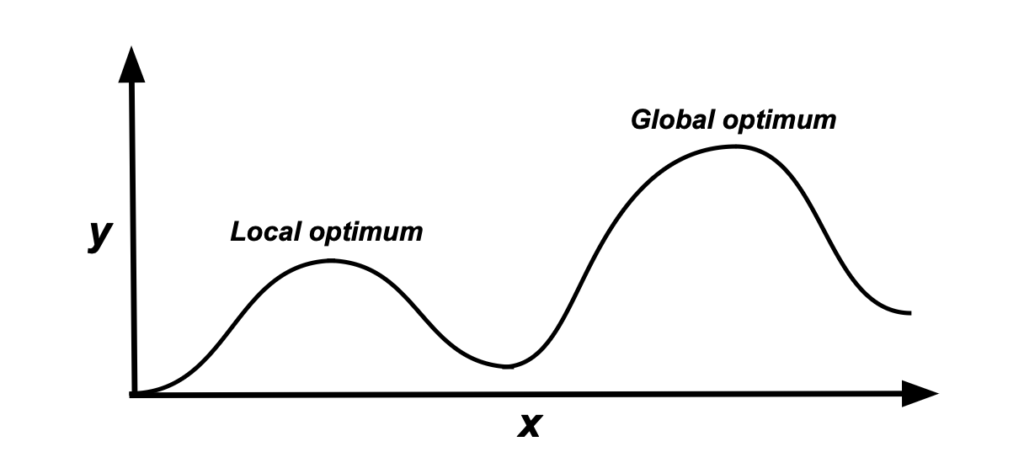
Alla värdena på X motsvarar här vår tillståndsrymd, tex 0-100. För varje tillstånd (alltså varje värde på X ) kan vi alltså räkna ut hur “bra” vi tycker att just det tillståndet är och kan sedan jämföra med hur “bra” ett annat X-värde är. Vi kan sedan med hjälp av olika AI-sökalgoritmer flytta oss längs med X-axeln åt höger eller vänster under vår jakt på det “bästa” X-värdet, dvs det X-värde som har det högsta Y-värdet.
I mer verklighetsnära problem är det dock oftast inte bara en variabel (som här X ) vi söker igenom utan det kan vara ganska många.
I grafen ovan framgår också varför det kan vara svårt att hitta den allra, allra bästa lösningen. Om vi börjar vår sökning nära ett lokalt optimum så kommer vi att röra oss mot det och inte mot ett globalt optimum som är en bättre lösning på vårt problem. Men inom optimering nöjer vi oss ofta med lokalt optimala lösningar.
AI-sökalgoritmer
Baserat på egenskaper hos problemet man försöker lösa finns det ett antal standardiserade AI-sökalgoritmer man kan nyttja som tex Hill Climbing eller A* (A-star). Det är dock inte där svårigheten med optimering ligger. Svårigheten är att reda ut problemets egenskaper och att implementera dessa på ett bra sätt.
Egenskaper
När man börjar titta på ett optimeringsproblem finns det ett antal egenskaper som avgör hur man ska angripa det.
- Känner vi till start- och sluttillståndet?
- Är det viktigt att vi kommer ihåg “vägen” från start till slut?
- Finns det några hårda och/eller mjuka krav på lösningen? Hårda krav är krav som lösningen måste uppfylla medan mjuka krav är egenskaper som avgör om en lösning anses bättre än en annan.
- Hur kan man representera en lösning på ett effektivt sätt? Är det exempelvis en lista av hållplatser eller vägnummer man sparar för en lösning på ett ruttproblem.
- Hur går man från en lösning till en annan, dvs vilka operatorer applicerar man på en lösning för att hitta dess “grannar” eller närliggande lösningar?
Egenskaper för ruttoptimering
För olika typer av ruttoptimering vet vi oftast både var vi börjar och slutar och det är vägen mellan start och slut som är lösningen vi söker och försöker optimera. Hårda krav kan till exempel vara att ankomsttiden måste vara före ett visst klockslag. Ett mjukt krav kan vara att minimera väntetiden vid eventuella byten.
Representationen av en potentiell lösning kan vara en lista med avgångar, där varje avgång innehåller:
- datum, tid, linje, riktning, och hållplats för starten
- datum, tid och hållplats för destinationen
I praktiken innebär det troligen att en lösning består av en lista med IDn som identifierar en specifik avgång.
Egenskaper för schemaläggning
Däremot för schemaläggning är vägen till en lösning helt irrelevant, det finns varken något start- eller sluttillstånd. Det enda vi vet är att en lösning kan vara bättre eller sämre jämfört med en annan lösning.
Ett exempel på ett hårt krav för schemaläggning kan exempelvis vara att någon i personalen är ledig en viss dag och om en lösning då har schemalagt den personen på en sådan ledig dag är uppenbarligen den lösningen ogiltig.
Ett mjukt krav skulle kunna vara att alla ska komma så nära sina avtalsmässiga procent som möjligt. Om någon är anställd på 40% men schemaläggs till 39% i en lösning och 50% i en annan så räknas den första som bättre, men båda är giltiga.
En lösningen kan representeras med IDn för personalen i samma ordning som man representerar de arbetspass som ska fyllas.
Egenskaper för måltidsplanering
Även för måltidsplanering är vägen till en lösning irrelevant. Man börjar med en slumpmässig lösning som man förändrar i flera steg för att förbättra den, men hur dessa steg ser ut är i slutändan ingen intresserad av.
Ett hårt krav skulle i detta fall kunna vara att inget recept från receptdatabasen förekommer flera gånger i samma lösning (dvs under samma måltidsdag) – en lösning skulle annars kunna föreslå att man åt gröt 6 gånger om dagen…
Ett mjukt krav kan vara att det total kaloriintaget för en hel dag med 6 måltider ska komma så nära ett visst värde som möjligt.
En representation av en lösning kan vara en lista med 6 IDn för de måltider som valts ut.
Sammanfattning
I denna artikel har vi utforskat hur AI kan användas för att lösa olika typer av optimeringsproblem, från schemaläggning av personal till ruttoptimering och måltidsplanering. Vi har beskrivit hur dessa problem kan bli mycket komplexa och hur AI-sökalgoritmer används för att hitta tillräckligt bra lösningar inom en stor mängd möjliga alternativ, den så kallade tillståndsrymden.
Vi gick igenom de unika utmaningarna och egenskaperna för varje problem. För schemaläggning krävs det att man tar hänsyn till personliga preferenser och regler, medan ruttoptimering handlar om att hitta den snabbaste och mest effektiva vägen. Måltidsplanering fokuserar på att skapa välbalanserade måltider utifrån näringsvärden och kaloribehov.
Sammanfattningsvis är optimering inom AI ett kraftfullt verktyg som gör det möjligt att lösa komplexa problem genom att hitta lösningar som kanske inte är perfekta, men som är tillräckligt bra för att möta de krav och mål som ställs.

Bra information & trevlig läsning!